「丸暗記」と「理解の伴う記憶」の使い分け

読者様よりご寄稿いただきました。

こちらに掲載いたします。

事の発端

定期テスト前に、父親である私が息子に対して

「テスト範囲の丸暗記がすべて。極端な話、例えばりんごの絵が何ページに載っていたか？が問われても文句は言えないぞ。東大王みたいなものだ。」

と言ってしまったのである。

私なりの言い訳はある。

繰り返し学習していると、「キーワードが、何ページぐらいかの右のページの上の方に書いてあった」とか、そのレベルまで覚えているものなのだ。

しかし本来なら、「テスト範囲をすべて理解し、出題者側（先生）の立場にたって、記憶すべきものはしっかり記憶しておきましょう。」とでも言うべきだったのかもしれない。

後述しますが、出題者側の意図を汲むことは重要だと考えています。

暗記と理解

Wikipediaには次のように記されています。

暗記（あんき, 諳記）とは、書いてある文章を見ないで口に出して言えるようにするために覚えること。記憶法の一種である。
一般にさまざまな意味で用いられる。暗記という言葉の用法を大まかに分類すると、理解の伴う記憶とほぼ同じ意味を表す場合、サヴァン症候群のように理解の伴わない記憶を表す場合（丸暗記）の2通りある。

理解（りかい）とは、物事の道理を悟り、知ること。また意味をのみこむこと。

理解の伴わない記憶の例

殊更に議論するつもりはありませんが、テストでそっくりそのまま出題されるとわかっているものに関しては、語呂合わせを使ってでも暗記した者が勝者となります。

問題：球体の表面積の公式は何でしょう？
対策：心配あるある
答え：$4\pi r^2$

（https://study-line.com/kukanzu-kyu/）

「丸暗記」と「理解の伴う記憶」の使い分け

では、「丸暗記」と「理解の伴う記憶」をどのように使い分けたら良いのでしょうか？読者様の考えるヒントになることを期待しつつ続けます。

4は、自然数また整数において、3の次で5の前の数である。(Wikipedia)

円周率とは、円の直径に対する円周の長さの比率のことで、数学定数である。通常、ギリシア文字$\pi$で表される。(Wikipedia)

半径を文字で置くときは radius の頭文字をとった省略形の $r$ とするのが典型的である。(Wikipedia)

自乗とは、ある数を自らと掛ける演算、あるいは演算によって得られる数を指す。二乗（にじょう）、平方（へいほう、英: square）とも呼ばれる。(Wikipedia)

上の説明は、Wipikipediaの文章の一部をコピペしただけなのですが、見るだけなら一瞬です。わざわざ時間をかけて、４つの文章を丸暗記する人はいないでしょうし、$4\pi r^2$を丸暗記するにしても、上記４つの概念を理解していることが大前提なのです。さらに、この公式を勉強している段階であれば、ほとんどの人は、円の面積=$\pi r^2$を理解していることでしょう。

では、$4\pi r^2$の丸暗記であなたの心は満足するでしょうか？（満足するのであれば、話はこれでおしまいです。）

知識の「丸暗記」で良い？

Google検索したらすぐに答えが見つかる小さな知識を「丸暗記」させ解答させることに、出題者は価値を見いだせるのか？

「公式$4\pi r^2$に関して知っていることを何でも書きなさい。」

こんなテストがあると面白いと思います。出題者側になって考えてみると良いですが、想像もしなかった解答、舌を巻くような解答がなされて初めて、出題者本人の心が動くわけであり、目先の点数がどうのこうのという話ではありませんが、ある意味、新しい概念を生み出す瞬間なのかもしれません。

球面の表面積

半径 $r$の球面の表面積=$4\pi r^2$で与えられる。この公式の最初の発見者アルキメデスは、外接円筒の側面への射影が面積を保つという事実から公式を導いた。(Wikipedia)

$2\pi r \times 2r=4\pi r^2$

公式の丸暗記で満足できない人は、上記のアルキメデスの説明を、丸暗記ではなく、理解できるように努めましょう。専門的な文章を理解し、自分の言葉で置き換え、お友達に説明できることが目標です。ただし、時間は有限ですので、理解し難い場合、一時的には、理解の保留もありでしょう。

台北101のチューンドマスダンパー

私だったら子供たちにどのように説明するのだろうか、と年末に自問自答していました。アイデアをあたためつつ、大晦日にチューンドマスダンパー という物体をWeb見つけましたので紹介します。

風による振動を緩和する目的のみで巨大なTMD（チューンドマスダンパー）が設置されている。マスダンパー全体の重量は660トン、最大一枚あたり直径5.5メートル、厚さ12.5センチメートルの輪切りの鋼板を、41層を重ね溶接して球状にし、92階から長さ42メートル、4本ごとに束ねられている太さ直径9センチメートルのケーブル計16本で吊っている。そしてこのマスダンパーの効果で、理論上は風力による振動を最大40%抑制できる。(Wikipedia)

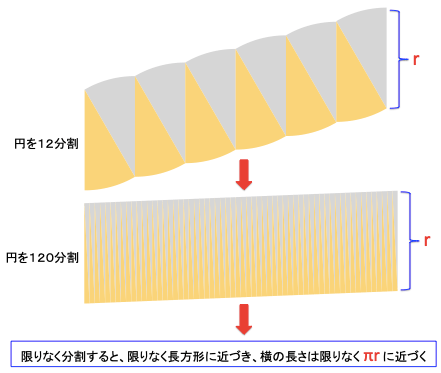
ここでは、「上記文章中の輪切りの鋼板=円柱」と考えてみましょう。以下、球体の表面積の私なりの説明です。

考える球体の半径を$r$とします。

（１）上から観察する→円柱の数によらず、上側の面の面積の合計は$\pi r^2$である。下から観察する
→同様に、下側の面の面積の合計は$\pi r^2$である。

個々の円柱の高さを限りなく小さくして、限りなく円柱の数を増やしいくと、限りなく表面は平滑になり、限りなく球体にに近づくが、変わらず、上側の面の面積の合計は$\pi r^2$のままなのである。

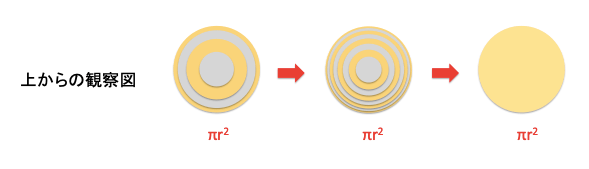
さて、水平方向から観察する側面の面積をどのように攻略するのか？

（２）限りなく球体に近づいた物体を、（限りなく球体であるのであるから、球体そのものだとみなした上で、）９０度横に傾け、（１）の逆の工程を辿ると理解できるはずである。個々の円柱の軸を長くし、円柱の数をだんだんと少なくしていくと、球体の表面は粗くなり、チューンドマスダンパー が９０度横に傾いた状態になるが、(1)と同様の考え方で、水平方向で観察した場合の面積は$\pi r^2$である。（左右で$2\pi r^2$）

（３）(1)と(2)より、

球体の表面積 $=\pi r^2 \times 4=4\pi r^2$

とみなすことができるだろう。

【余談】人の心を動かす

私の高校時代の話です。

勉強とは関係のない話です。

保健の教科の定期試験で、学年トップが100点、学年２位が99点だったことがあります。具体的に書くと身元がバレるでやめますが、学年トップの女の子は芸術系に進み、99点の男の子は医学部に進みました。両者とも私に近い存在だったので、筆跡を知っているのですが、イメージとしてはこんな感じです。

高校の保健の先生が、右側のような筆跡の男の子が書いた99点の答案を見て、とても悔しがっていました。100点をあげたいぐらいだと。受験勉強の本質的な話でないかもしれませんが、今現在に役に立つとは思えないようなことが、将来役に立つことがあるものです。お医者さんになった今、この几帳面さが、手書きの指示書などの正確さに繋がっているかもしれませんし、ひいては、パラメディカルから信頼されていることでしょう。

ちなみに、息子は、左のような字を書きます。独特な字ではあるけれども、読書感想文を丁寧に仕上げて、その手書きの感想文はその後、審査員にまわされます。それが毎年毎年続くわけです。おっ！この子（読書感想文の審査時は、書き手の名前は伏せてあるはずです）の感想文だぞ！じっくり読んでみよう！となるかもしれませんね。

管理人より

新年のご投稿、嬉しく拝読いたしました。

私も学生時代に立体の表面積についてあれこれ考えたことがあり懐かしさを覚えました。球の場合は円柱に投影する話をよく見かけますが、本当にそうなのか同期と熱く議論した記憶があります。
台北101は台湾留学時によく眺めていました。恥ずかしながらダンパーの存在は知らず、勉強になりました。ありがとうございます。

今年もよろしくお願い申し上げます。

追記
記事中の図はご投稿してくださった方のオリジナルなもので、台北101のダンパーの色に合わせてくださいました。弊サイトのメインカラーとも合致しています。

追記2
記事内の数式は$\LaTeX$記述法をJavaScriptを用いて読み込ませました。美しさにちょっとだけこだわりました。コード記入ミスがあったらすみません…。

追記3
$\LaTeX$は高2の夏休みを使って勉強しました。この世で最も美しい記述法だと言われています。例えば、次のように異なります。

↓普通に書いた場合
2πr x 2r = 4πr^２

↓$\LaTeX$を使った場合
$2\pi r \times 2r=4\pi r^2$

けっこう違いますよね。（えっ、あまり変わらない！？）

追記4
$\LaTeX$記述法は少し面倒に思えますが、複雑な数式でも綺麗に表現できるメリットがあります。
例えばこんな感じ。

\begin{eqnarray}
\sum_{ k = 1 }^{ n } k^2
= \overbrace{ 1^2 + 2^2 + \cdots + n^2 }^{ n }
= \frac{ 1 }{ 6 } n ( n + 1 ) ( 2n + 1 )
\end{eqnarray}

こんなのも、

\begin{eqnarray}
\Delta \varphi
= \nabla^2 \varphi
= \frac{ \partial^2 \varphi }{ \partial x^2 }
\frac{ \partial^2 \varphi }{ \partial y^2 }
\frac{ \partial^2 \varphi }{ \partial z^2 }
\end{eqnarray}

やりたい放題できます。

サイトで用いる場合は、<head>タグ内と記事内に数式を読み込むことを宣言（JavaScriptを用いてコード記述）すれば表示されるようになります。