フィボナッチ数列・リュカ数列・・・黄金比

フィボナッチ数列・リュカ数列・・・黄金比
フィボナッチ数列はご存知の人が多いと思いますので、突然ですが、リュカ数列の定義を載せてみます。
0,1,1,2,3,5,8,13,21,34,55,89…と続くフィボナッチ数列と何が一緒で何が違うのかと疑問に思う人がいるかもしれません。
フィボナッチ数列の初項が「0」で定義され、リュカ数列の初項が「2」で定義されることが大きな違いですね。そうならば、初項を0から9まで試してみたくなるものです。以上表にしてみました。
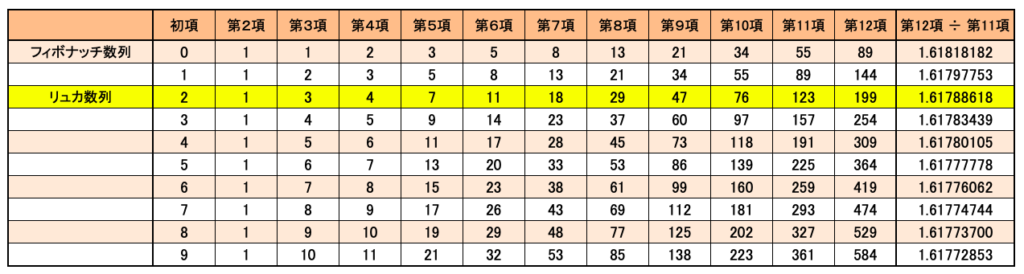
この程度の簡単な表ですが、作成してみる価値はあったようです。この記事を書くにあたって、インターネットの記事をいろいろと眺めてみましたが、フィボナッチ数を神秘的な数字と捉えている人が多いのです。しかしながら、初項がどんな数字であれ、隣接する2項の比が黄金比に収束していくという事象を見てしまうと、その面白さに心は動かされる一方で、一つ一つの数字としてのフィボナッチ数に特別なものはないように感じました。
リュカ数列の美しさ
遊び心で、初項が「1」で、黄金比を掛け続けてみました。結果は下の表の通りですが、数字が大きくなるにつれてリュカ数列に一致していく様子がわかります。不思議ですね。

英検で必要とされる語彙数〜黄金比に近似〜
ちなみに英検で必要とされる語彙数は以下の表の通りです。単純計算ですが、5級の学習時間の24倍の時間をかけると1級に到達しますね。(14400÷600=24)実際には、将来の職業での必要性や大学の受験科目の難易度にも左右されますから、計画には柔軟性が必要です。

英検の事業沿革を見てみますと興味深い文章がありました。
1987年
準1・5級新設
1・2級間の程度差を適正化するための準1級と、初級学習者を対象とした5級が新設され、英検は6つの級に。
1994年
準2級新設・第1回「児童英検」実施。2・3級間に準2級が新設され英検は7つの級になり・・・
最初は、1級、2級、3級の3つだったらしいのですが、4級が追加され、1987年に準1級と5級が追加され、1944年に準2級が追加されたのです。
上記の表の「必要とされる語彙数」を見ると明らかですが、準2級と準1級が存在しなければ、3級から2級、2級から1級のそれぞれで、大きなギャップが生じてしまいます。そして、その問題点を解決すべく、準2級と準1級が創設されたとするならば、ここに黄金比の必然性が見て取れる、ような気がします。
興味深いことに、英検のサイトには、「例えばある受験者が英検®2級を受験し4技能の合計スコアが2,500点としましょう。上図で示すとおり2,500点というのは、準1級の合格ラインである2,304点を超え、この受験者は、準1級に合格できる能力が備わっているというのが分かります。このように現状の能力と受験の上位級のスコア差異から現状の能力把握の目安としてもご活用いただけます。これは下位級についても然りです。」という記述があります。
あくまで私の妄想で、深追いするつもりはありませんが、仮に合格基準を得点率61.8%としてみます。当該級で得点率100%の場合に、記事によれば、その上位級の合格基準に到達するだけの力が備わっているわけですから、その比率は黄金比そのものなのです。
そもそも、英語をはじめとする学問において、検定試験の級ごとに、明確な境界があるはずがありませんが、学習計画を立てる上で、上記のことは参考にすべきだと思われます。
英検の学習計画の再考
英検の回しものではないのですが、乗り掛かった船なので、最後まで書いてみます。もちろん、英検なんぞ関係なくても、学力を上げていくモチベーションがあれば、それはそれで良いとは思いますが、英検取得をペースメーカーとして学力を上げていく戦略も悪くはないでしょう。
以下、黄金比から導き出される英検の学習の考え方です。例えば、高校に入学してから間も無く、学校の先生から英検2級合格のための学習計画をたてなさいと言われたとしましょう。その時の考え方で重要だと思うことは、5級から準2級までを満点取れるだけの基礎学力は確固たるものであるかということです。
もっともそれぞれの級に明確な境界を決めることには、英語学習という観点からは意味がないことなので、その辺は曖昧さがあって構わなくどんな方法でも良いのですが、最高水準特進問題集、シリウス発展編Vol3、もしくは、Progress in English R Book3のレベルまではマスターしているでしょうか、ということでしょう。そして、その部分こそが、61.8%を占める部分なのです。残りの38.2%は、2級の過去問を使って、語彙力強化や演習で埋めていくのです。そして、その努力は、さらに上の級の学習の足がかりとなることでしょう。
別の表現で書きますが、英検2級対策として、怪しげな予想問題集を解く必要はないと考えています(真の学力の観点から、やってもやらなくても同じだからです)。あくまで岩盤のような基礎があってこその2級対策であり、その2級対策に関しても、語彙力強化や演習目的で十分な量の過去問を課した方が良いと考えています。
以上の概念を図にしてみました。
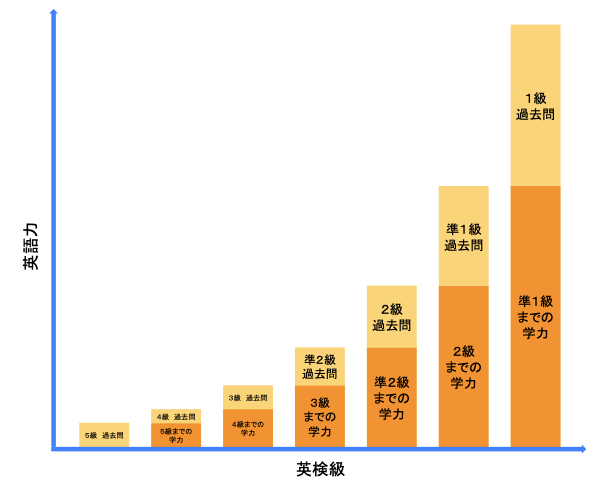
話変わりますが、英検2級を受けさせられたという、ガクさんの灘高校のエピソードは参考になります。日本のトップ層のレベルを知る手がかりになるからです。妄想ですが、灘高校からの入学組に対しては、「英検2級合格(センター試験の平均点)の力は既にありますが、さらに磨きをかけましょう。」ということでしょうし、灘中学校からの持ち上がりの生徒に対しては「高校進学を機に、準2級相当までの復習をしておきなさい。」ということかもしれませんね。
ちなみに、中学3年生の時に英検2級を取得した息子に聞いてみると、感触として、九州の私立難関高校2校の入試過去問は、準2級~2級に相当するのではないかと言っていました。
0から1を生み出す方法
上のグラフを注意深く見てみると、英検5級にはオレンジ色の基礎の部分がありませんね。それもそのはず、英検は5級からスタートするからなのです。学習のやりかたを理解しや学習リズムが整いさえすれば、家庭学習で少しずつ級を上げることが可能でしょうが、最初はうまくいかないかもしれません。ドミノ倒しのように、最初だけは外部の力(学校の授業など)が必要かもしれない、とこのグラフは語っている気がしました。小学校から本格的に英語の授業が始まるらしいのですが、小年生の子を持つ親としては、まずは子供の英語への関心度を見る目的で、宿題等のサポートをしながら、折をみて、英検5級の過去問をさせてみると良いのかもしれません。学習者との相性もあるのでなんとも言えませんが、その後は、Progress in Englishを使い、基礎学力の向上(グラフのオレンジ色の部分)に努めるとともに、語彙力向上や演習を目的に、英検の過去問(薄いオレンジ色の部分)を投入していくと良いでしょう。
最後に人生訓!?
ガク氏のこの言葉にハッとさせられました。人生のマイナスの定義は曖昧なものですが、何らかの理由で「現在の項」が大きくマイナスになってしまったとします。この溜まりに溜まったマイナスをプラスに転換することはできるのでしょうか?そんなことを考えてしまいました。
仮に、人生においても、特に大きな力が働かない限り、前の2つの項の和で、次の項になるとしてみましょう。では、溜まったマイナスをプラスに転換するには、前項に対して、どの程度のプラスの力が必要なのでしょうか?では、下の表とグラフを見てください。
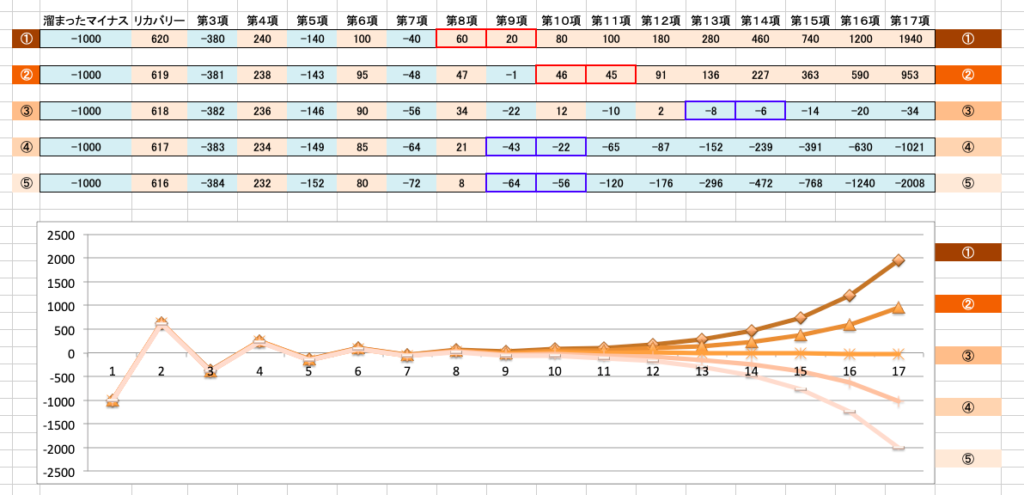
初項(溜まったマイナス: -1000)に対して、第2項(リカバリー)では「黄金数の逆数 x 1000」に近い値を設定してみました。第3項以降は「前の2つの項の和」としています。面白いことがわかりましたね。マイナスとプラスが交互になっていたものが、①の場合には第9項以降で、②の場合には第11項以降で、プラスに転換されています。
黄金数の逆数$={\frac {-1+{\sqrt {5}}}{2}}=0.6180339887・・・$
以上、一般項を式で表すことは可能なはずですが、話が難しくなるのでここまでにしておきます。逆に言えば、高校数学などで難解な数式を理解できない際には、具体的な数字に置き換え、上記のような分析をしてみることは有効な手段だと思います。また、スマホ、タブレット全盛の令和の時代ですが、スマホ代に月々払うお金があったら、10年落ちの中古のパソコンでも良いので、使い勝手の良いものを入手してもらい、学習に活かしていくべきだななんてことを考えてしまいました。
新学期始まりましたが、どうぞご武運を。
余談 ABCモデル
この記事を書くにあたっての前提ですが、花弁の枚数は、植物によって様々なようです。ただ、植物分類の科によってはフィボナッチ数列に一致する場合もあるということでしょう。ですので、個々の植物ごとに花弁の発生のメカニズムを理解しない限り、いつまでも神秘的なイメージのままになってしまいますね。身も蓋もない話ですが、そのようにご理解ください。
http://had0.big.ous.ac.jp/gakunai/experiment2/kihonsuu/kihonsuu.htm
それはさておき、
とは面白いですね。
https://nadatodai.com/contribution-2203-4/

好奇心の赴くままですが、気になったので、少しだけ勉強してみました。大学受験を控えるお子様の前では慎重にコメントしなくてはなりませんが、高校生物で習うもので、花の発生におけるABCモデルというものがあります。詳しくは「https://ja.wikipedia.org/wiki/ABC%E3%83%A2%E3%83%87%E3%83%AB」を参照して頂くとして、まずは、下記の図で示されるモデル図を見てください。
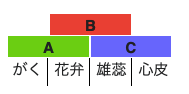
がく、花弁、雄蕊、心皮は、基本的には、A、B、Cという3種類の支配者(マスター転写因子群)によって支配されていますが、そのA, B, Cが出現する場所(発現する場所)はあらかじめ決まっています。(そういう前提で話をします。)
その支配下では、例えば、Aの発現領域では「がく」「花弁」のいずれか、Cの発現領域では「雄蕊」「心皮」のいずれかが形作られる運命にあります。また、AとCはライバル関係(お互いに発現を抑制し合う関係)だそうです。
その両者に関わっているのがBですが、実は、「花弁」が形作られるためには、Aに加え、Bの協力者が必要だということなのです。
ABCモデルからの発展
最初に述べましたように、詳細には、個々の植物のメカニズムを理解し記述しなければいけないでしょう。一方で、高校生相手には、高校生物の教科書に従った典型的な用語を使って説明しないといけないでしょうが、そんなことを言っていては面白みが失われるので、もう少しだけ進めてみます。
では、下の図を見てください。
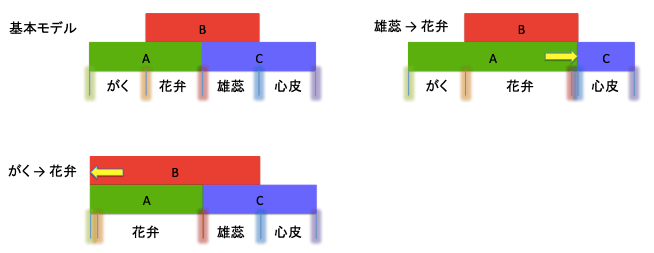
- (雄蕊→花弁):何らかの理由で、相対的に支配者Aの力が強くなり、Aの支配が右(花の内側)に広がることになったとします。そうなると、本来「雄蕊」になるべき場所に「花弁」が出現すると考えることができます。
- (がく→花弁):何らかの理由で支配者Bの支配が左(花の外側)に広がれば、本来「がく」になるべき場所に「花弁」が出現すると考えることができるのかもしれません。
まあ、基本モデルから出発し、いろいろなアイデアは出てくるものですが、空想があまりに過ぎるわけにはいきませんので、この辺で終わりにします。
—————
the end
管理人より
フィボナッチ数列と初めて出会ったのは小学4年生の頃だったと記憶しています。父の書棚に「算数・数学ランドおもしろ探検事典」という本があるのを見つけ、ひたすらノートに書き写していました。学校で習わないことがたくさん載ってあり、驚いたのを覚えています。
そのあと、「数の悪魔」を紹介されてのめり込むように勉強しました。
中学受験に向けて勉強していた頃、上記の本で紹介されていた事項をテーマにした問題と出会うことがたびたびあり、君はこんなところにいたんだねと懐かしさを感じることもしばしば。
中学入学後は同じく数学好きの友人とひたすら数学の話をしていました。
それにしても、黄金比を掛け続けるとリュカ数列に近づくとは面白いです。
また、英検の達人であるご投稿者からの考察も興味深いです。
英検は高校1年生頃に初めて受けた記憶があります。灘高で全クラス一斉に2級を受験しました。なぜ、そうなったのかいまだに不明です。検定とは無縁な家庭で育ったため、何から何まで新鮮でした。この頃になって、数学検定なども存在することを知りました。
余談
$\LaTeX$記述法で数式を記述してくださりありがとうございます。大変助かります。
余談2
「前の2つの項を足すと現在の項になる」とは、私たちの日々の行動や人生選択についても当てはまりそうです。
管理人より 2
追記ありがとうございます。
灘高での英検一斉受験については、新高と在来生の英語力の違いを客観的な物差しでみたいという先生の思惑があったのかもしれません。私の学年団の英語担当は「東大英語リスニング」や「ユメタン」で有名な先生でしたので、書籍執筆に向けたデータ収集の一環だったのではないかと思ったりします。
灘の場合、新高は英語ができるが数学が遅れている。在来は数学が進んでいるが英語が遅れている。…とよく言われており、他教科の先生も英検結果に関心を示していました。
ご子息からも意見いただきました。
当サイトの読者は九州在住の方もたくさんいますので、大変参考になります。ありがとうございます。
管理人より 3
追記ありがとうございます。
初項をマイナスで始めたときの挙動をグラフで示すことで、さらに面白くなってきました。
記事前半で黄金比に収束する例がありましたが、第2項次第で状況は一変することが視覚的にわかりやすいです。
後日、改めてコメントを掲載いたします。
管理人より 4
さらなる加筆ありがとうございます。
ABCモデルはよく目にします。
昨年、上野にある国立科学博物館で植物展(特別展)が開催されていました。植物は私の大好きな分野ですので、大学の知人らと訪問しました。植物の神秘に迫ろうというのがテーマのようで、さまざまな植物が展示されていました。その中にABCモデルについて解説したコーナーがあり、大きなポスターとともに器官の様子が少しずつ異なる花が展示されていました。
また、中学入試にABCモデルが出てきたこともあります。私は講師として解説する側でした。大問まるまる1つが当てられており、出題者の熱意が感じられました。問題文が長く、最後の大問ということもあったのか、手をつけた生徒は少なかったです。聞いたところ、「難しそうに見えたから」とのこと。しかし、問題文の誘導が親切なため、丁寧に読み解けば確実に正答できる問題であり、挑戦して欲しかったところです。処理能力が高く時間に余裕のある受験生は、こういった問題もしっかり得点するのでしょう。
話は変わりますが、ABCつながりで。日曜日(2022.04.10)の夜にNHKでABC予想の番組が放映されました。普段はテレビを見ませんが、大学の先輩が番組制作に関わったとメールで知らされ、家族で見ました。恥ずかしながら理解が追いつきませんでしたが、ABC予想の証明は史上稀に見る大変革をもたらすようで、フェルマーの最終定理も瞬時に解決するようです。
詳細はNHK番組ページに載っています。
数学者は宇宙をつなげるか?abc予想証明をめぐる数奇な物語(前編)
関連書籍
数の悪魔
一時期、有名になりましたね。
大人も子どもも心から楽しめるところに本書の良さがあると思っています。


コメント