円周率がπではない世界

円周率が$\pi$ではない世界

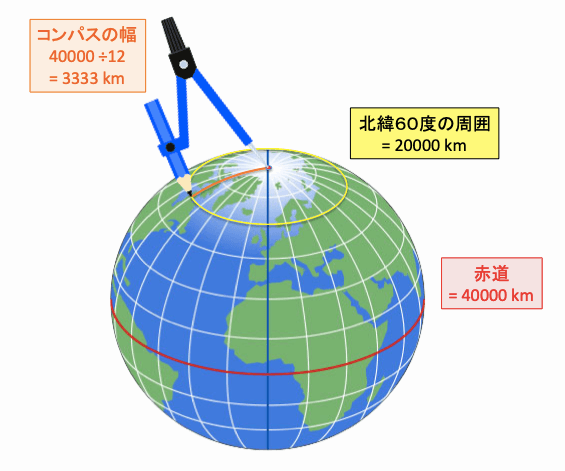
円周率=２の世界：巨大なコンパスを使って、北極点を中心に半径10000kmの円を描くと、赤道上を一周する。→ 円周÷直径＝２である。
円周率=３の世界：巨大なコンパスを使って、北極点を中心に、半径3333kmの円を描くと、北緯６０度線上を一周する。→ 円周÷直径＝３である。
奇妙な説明だと思われるかもしれませんが、平面ではなく、球面で円を描く限りはこの説明になってしまいます。地球表面上で円を描く限り、円の大きさによって、円周÷直径の値は変化しますよね！？

https://www.homemate-research-junior-high-school.com/useful/20100_junio_study/1_geography/earth/

では、$\pi$は何を意味しているのでしょうか？

→上記説明とは逆に、球面ではなく、平面上の半径と円周を考えているから、円周率＝$\pi$なのです。

平面（へいめん、plane）とは、平らな表面のことである。平らな面。一般的には曲面や立体などと対比されつつ理解されている。(Wikipedia）

三角関数を使って式を一般化してみる

次のように考えることもできます。

例えば、勉強机のような小さな世界では、3.1415926535・・・という感じに、円周率≒$\pi$と見做すことができるのかもしれません。地球の大きさに対してミクロで、平面に近い世界だからです。このように考えると、限りなく北緯90度に近い緯線上の円を描くことで、北極点を中心とする円の円周率を限りなく$\pi$に近づけることができるでしょう。

http://koukoujukenshakai.g2.xrea.com/chiriroom/chiri1/chiri1-c-1.html

以上、上記図を参考にしながら、数式にしてみました。

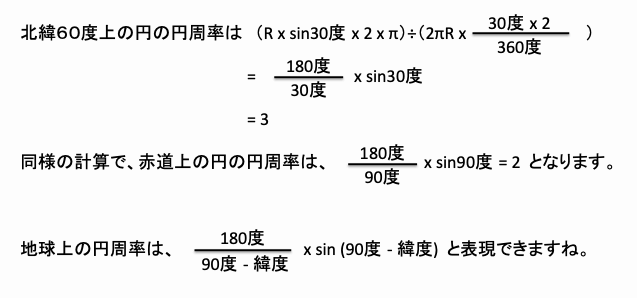
独自のアイデアでここまで書き上げたところで、アルキメデスの足元にも全く及ばないという現実はありますが、こういう思考は、地図の理解には役にたっているのかもしれません。

正距方位図法

最高水準特進問題集の地理の問題から抜粋してみました。

この問題の正答率なんぞ知りませんが、内訳を考えてみましょう。

真面目に授業を受けてきた人は、「中心からの方位が正しい正距方位図法だから、中心である東京からX軸の正方向に線を伸ばし・・・」

と素直に答えることができるでしょう。

私は不真面目ですので、次のようなことを考えてしまいそうです。

「まっすぐに進むと宇宙空間に飛び立ってしまいますよ」

大阪人は、地理にかけて「チリ！」と答えるかも！？（ガク氏談）

少々真面目な話をすると、この手の問題は、本来は、地球儀を観察しながら、理解すべき問題かもしれません。球面で東京とチリを線でつないでみたりするのです。

言葉の定義の理解も重要です。東西南北とは何か、角度とは何か、直線、平面、球面・・・

さらに、「何を見ているのか」です。机上の平面なのか、地球なのか、宇宙空間なのか。

上記入試問題の場合は、地球の理解があっての正距方位図法ですが、当然、宇宙ではありません。

そんなことをすべて考察し理解し、その上で「チリ」と答えられる人は、灘中合格者には多数いることでしょうね。

【追記】円周率が〇〇より大きいことを証明しなさい

円周率が3.05より大きいことを証明しなさい

「円周率」をキーワードに何気に検索してみたら、東大の入試問題がでてきました。私は東大入試を経験したことはなく、学力的にも程遠い人間なのですが、東大でこんな簡単な問題がでるものかとちょっと不思議な感じがしました。

頭の片隅に入れながら、仕事の合間に考えてみました。円に内接する正１２角形なら解けるに違いないと確信して、いざ先ほど鉛筆を動かしてみると、すんなり解けました。もちろん、入試本番に力を発揮できるかは、いろいろな要素があり、別問題ですが。

世の中には、私と同じような証明をしている人がごまんといることでしょう。中学入試対策と、簡単な中学数学の知識で解けてしまうと感じました。それとも、何か私の見当違いでしょうか？難関中学入試、難関高校入試を経験した人が、いざ東大入試になった時には頭が硬くなるのでしょうか？それを見抜いた上での入試問題なのでしょうか？

どこにでもありそうな説明をここで書くのも憚られますが、乗り掛かった船なので、図を作成してみました。計算をしやすくするために、半径を２としてみました。以下、図を見ながら理解をしてみてください。

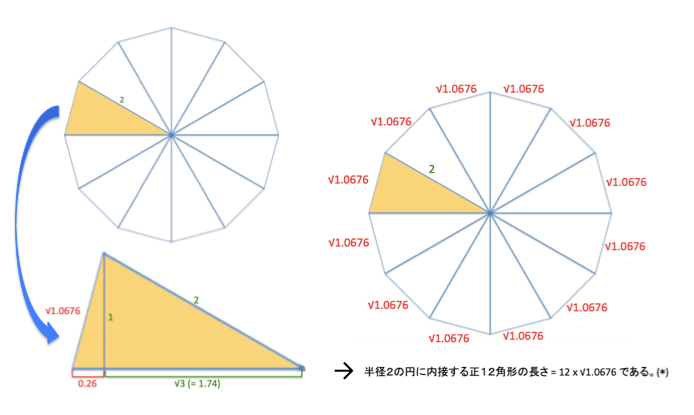
最終的には、(*)の二乗の値が、(半径 x 2 x 3.05) の二乗の値よりも大きいことを計算で示せば良いでしょう。

(*)の二乗 = 12 x 12 x 1.0676 = 153.7344

(半径 x 2 x 3.05) の二乗 = (2 x 2 x 3.05) x (2 x 2 x 3.05) = 12.2 x 12.2 = 148.84

円周率が3.1より大きいことを証明しなさい

というものであれば、

 (*)の二乗 = 153.7344   ＜   (半径 x 2 x 3.1)の二乗=153.76

となり、証明が失敗に終わりますが、この問題の場合は、$\sqrt{3}$の近似値を1.733とすることで、回避できます。

 (*)の二乗 = 154.265616   ＞   (半径 x 2 x 3.1)の二乗=153.76

となり証明可能です。

この証明の肝は、直感的に「円に内接する正１２角形」なら行ける！と思えるかどうかでしょうか。如何でしょう。それと、$\sqrt{3}$の近似を1.74と試してみるさじ加減を自分に許することができるかどうか。言い換えれば、頭を柔らかくということですね。また、$\sqrt{3}$の近似値を、四捨五入ではなく、切り上げによって、1.74 または、1.733 とすることは証明をする上で重要なことだと思います。

「円周率が$\pi$ではない世界」を使った説明

最後に、「円周率が$\pi$ではない世界」の式で考えてみましたが、とても難解ですね。以下、googleで遊んでみました。

北緯66度の条件で、球面での円周率が3.05を上回ります。

北緯74度の条件で、球面での円周率が3.1を上回ります。

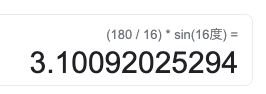
北緯87度の条件で、球面での円周率が3.14を上回ります。

内接正n角形での証明でも三角関数を使いますので、球体を使った説明は何ら新しいものではないと思われるかもしれませんが、実はこれ、似て非なるものなのです。詳しい説明は省きますが、sin24度、sin16度が出てくる内接正n角形は存在しないからです。（正６０角形の場合は、sin3度がでてきます。）

ただし、言葉は慎重に選びますが、受験では、そもそも平面上の円周率を論じているのですから、私の球面での説明がそっくりそのまま、「証明」にはならないかもしれません。思考は自由に、証明は慎重に、ということで…

まとめ

話がかなりずれてしまった感じはありますが、円周率が$\pi$ではない世界とは地球表面のことであり、球面の理解があってこその平面図の理解だと思います。

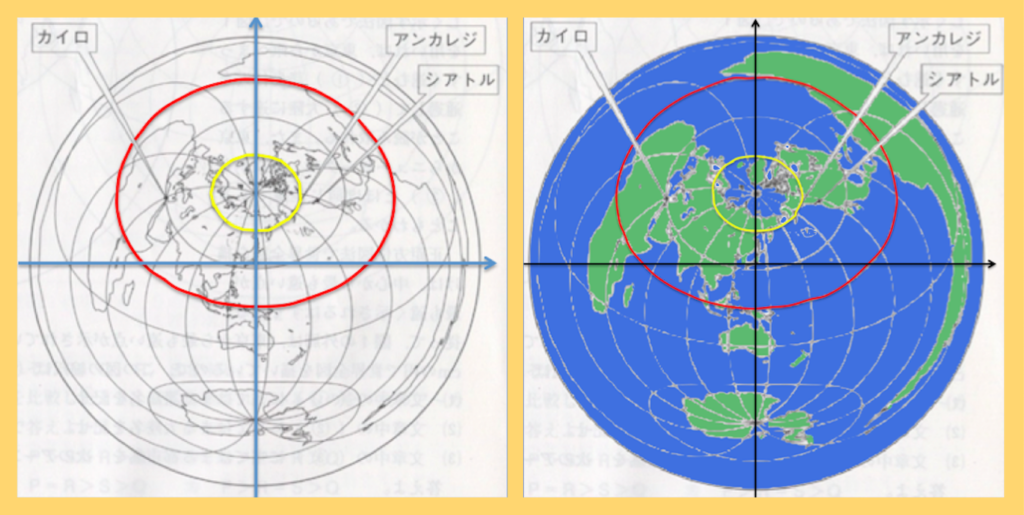
理解しやすいように、上記の正距方位図に北緯60度線（黄色）と赤道、XY軸を描いてみました。

「東京から飛び立った航空機がまっすぐ東に進む」とは、「原点（東京）から、たて軸（南北の軸）に対してのよこ軸（東西の軸）の正の方向（東の方向）に、球面に沿ってまっすぐ進む」と理解できていますでしょうか。

受験パズルの攻略法（https://nadatodai.com/contribution-2112/）の北海道振興局の話にも関連しますが、、単なる文字列または数列に止まらず、平面地図、海や山を意識するという意味での立体地図地球、宇宙空間にも意識を向け、総合的な理解に努めたほうが、記憶にも残りやすいと思いますし、学習が楽しくなるのだと思います。

追記　「緑化」が進むグリーンランド、世界に多大な影響及ぼす可能性

引用
（ＣＮＮ） グリーンランドの中で氷が失われた地域は、過去３０年間でニューヨーク市のほぼ３６倍に上ることが１３日刊行の研究報告で明らかになった。これらの土地は、湿地帯や低木地帯に急速に取って代わっているという。
引用終わり
https://www.cnn.co.jp/fringe/35215224.html

原著論文？
https://www.nature.com/articles/s41598-024-52124-1

いつかこういう話題で記事を書くことがあるかと想像していましたが…

あまりに大きすぎるテーマで、私には、良いも悪いも内容についてはコメントする能力がありません。しかし、世界地図の色は、今後、変わってくるかも知れませんね。

子供の頃に見た世界地図の配色では、南極とグリーンランドは、白。

https://ja.wikipedia.org/wiki/%E4%B8%96%E7%95%8C%E5%9C%B0%E5%9B%B3

上記「まとめ」を作成している頃に、南極とグリーンランドの色を「緑」に塗ったのですが、その想定時期は、私の死後でした。

ともかく、研究対象としては面白いのではないでしょうか。灘東大出身の研究者として、頑張ってくれる人が出てくるかも知れませんね。

管理人より

ご寄稿いただきありがとうございます。

数学と地理という一見全く別の分野がリンクされており、興味深く拝読いたしました。分野横断・融合型の学習はやっぱり楽しいです。

正距方位図法は問題文冒頭の「中心からの〜方位が正しい」をしっかり読み取りましたか？というような意図で出されたのでしょうか。大阪人の私は地理→チリに反応してしまいましたが…。

管理人より2

話がずれますが、地理は本当に好きでした。

地球儀や地図帳は一日中眺められる自信があります。上京する際も高校で用いた地図帳は忘れずに持参し、食事中にページをめくることも多かったです。

また、雨の日は山の地図を開いて計画を練ったりもしました。登山中も地図は肌身離さず持ち歩いていますから、私の生活からは切り離せないものです。

管理人より3

正距方位図法と地球儀の話ですが、次のような考え方もできそうです。

1. 緯線に直行し緯線上の任意の点を通る面は必ず球の中心を通る
2. 経線に直行し経線上の任意の点を通る面は必ず球の中心を通る

東京の真東の方向は、南北方向（経線）に直行する方向と言い換えられます。よって、距方位図法が提示されなくとも、上記2. の性質を用いることで（北半球である東京の裏側は南半球を通るため）およそチリが該当する（他の選択肢は消去できる）と回答できるでしょう。

（誤りがあればコメントでご指摘願います）

管理人より4

東大のこの入試問題は一時期有名になった記憶があります。

首都圏の中学受験塾で教えていた頃、授業時間に余裕が出てくると「雑談をして欲しい」と子どもたちから頼まれることが多かったです。そこで中学・高校で習うような内容を噛み砕いて教えていたのですが、東大の円周率問題は受けが良かったです。「円周率が3以上を証明せよ」と出したところ小学4年生でも説明できる人がいて驚きました。

管理人より5

グリーンランドについて追記いただき、ありがとうございます。

北極圏（とその付近）における温暖化の影響というと、私の後輩（高校・大学の）が現地の研究機関で調査しています。3ヶ月ほど前、彼が一時帰国した際に話をしましたが、土壌を採取しながら調べているようです。

関連記事

3月14日は円周率$\pi=3.14…$の日です。

東大生の独り言

今日はパイの日 | 東大生の独り言 読者様からエッセイが届きました。 パイの日 今日は３月１４日でパイの日ですね。http://www7a.biglobe.ne.jp/~pienohi/html/pai.html（上記記事に灘がでてきます。）円周...