【追記あり】受験パズルの攻略法｜目標達成のコツ

読者様より、受験攻略法についてご寄稿いただきました。

受験に限らず目標達成のプロセスに応用できると思います。是非とも最後までご覧ください。

いずれパズルは完成する

息子が中学生だった数年前、成績が停滞していいた時に、塾の担任から言われた言葉です。パズルは英語で難問という意味でもありますから、私は一瞬、良い例えだなと思いましたが、大昔に聞いたことがあるような気もしました。言い尽くされた言い回しなのかもしれないなと感じつつ、数年が過ぎ去り…

数年前の記憶を辿りつつ、コラムを書くにあたって、アイデアを発展させようと思います。

塾の先生の言葉

• ︎日々の授業を大切にし、ピースを揃えていくこと。︎
• カリキュラムを信じてほしい。︎
• いずれパズルは完成する。

息子の心に響けば良いですが、そうでないのなら、問題です。

私ならこのように助言したい。

受験までにやり遂げるべくテキストが決まっているのなら、最終的にそのテキストを完全攻略すれば良いのです。

その過程では、各自、攻略できそうなところからやっても良いのだと、と私は思っているわけです。低い次元で「気が向くままに、適当に、取っつきやすい単元の勉強をする」というニュアンスではいけませんが、高い次元に立ち、「俯瞰した上で、戦略的に、攻略できそうなところから始めて、陣取り合戦のごとく、領土を全体に広げていく」と思っていただければ良いと思います。

文字列ではなく地図パズルをイメージする

単なる思いつきですが、架空の問題で話を広げてみます。

問題：北海道の振興局をすべて覚えよ。

答え：そらち、いしかり、しりべし、いぶり、ひだか、おしま、ひやま、かみかわ、るもい、そうや、オホーツク、とかち、くしろ、ねむろ

空知　石狩　後志　胆振　日高　渡島　檜山　上川　留萌　宗谷　オホーツク　十勝　釧路　根室

仮名表記だと暗号のようで覚えるのはとても大変です。漢字で書いてみると、幾分わかりやすい気がしますね。小学生といえども数年後には大学受験を控えているわけですから、積極的に漢字で覚えた方が良いと思います。

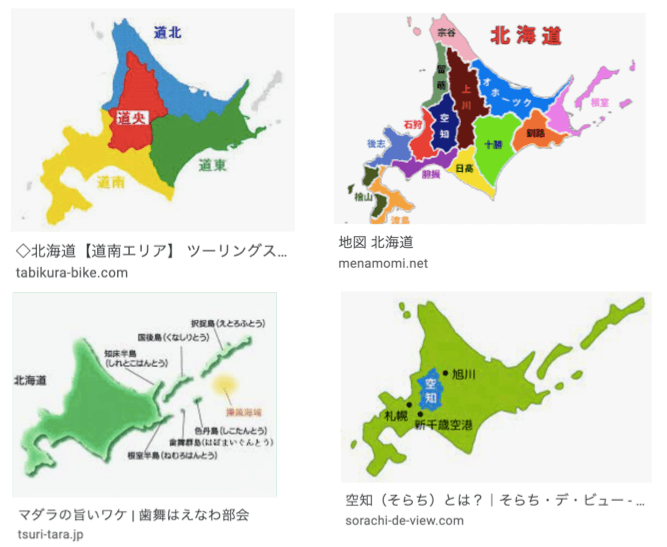
さてどこから攻略するか。私なら、宗谷（そうや）から攻めます。

1. 日本の本土における最北端の地であり、一般人が通常訪れることのできる最北端の地を宗谷岬という(Wikipedia改変）。左側（西側）は、留萌（るもい）。日本海側に位置し、ニシンの最大の産地である。右側（東側）には、オホーツク海に面しているオホーツク。根室（ねむろ）半島の先に、歯舞　色丹島が続く。
2. 北海道唯一の山脈、日高山脈の左側（西側）に、胆振（いぶり）・日高（ひだか）地方。その右側（東側）には、十勝（とかち）平野、釧路（くしろ）湿地と続き、根室（ねむろ）半島に繋がる。
3. 札幌市を有する石狩（いしかり）平野。石狩振興局は、北海道地方で最大規模の人口を有し、宮城県（約236万人）と同程度である。その右側（東側）には、空知（そらち）。人口第１の札幌と人口第２の旭川の間に位置する。旭川市を有する上川（かみかわ）盆地。石狩（いしかり）、空知（そらち）、上川（かみかわ）を留萌（るもい）が束ねる。
4. 小樽が属する後志（しりべし）、その下（南側に）は、檜山（ひやま）、渡島（おしま）である。以上全部で１４ピース。

最後に、以上（１）から（４）までの該当箇所を穴埋め問題にすれば良いのです。

専門家を差し置いて私が多くを語る資格はありませんが…、単純暗記の前に、ガク氏のように、日頃から地図を嗜むと良いでしょう。

平面パズルから立体パズルへ

中学受験を志すお子様なら、簡単すぎる問題でしょうか。

等差数列の和（合計）は（はじめの和＋さいごの数）x 個数 ÷２で求められる

この公式を覚えろ！と怒鳴り散らす親はいないとは思いますが…

この例にしても、平面図形を意識して理解したほうが良いと言えます。ただし、本文の左上の説明と、右下の図のイメージはリンクしにくいですね。裏返して右に９０ど回転させた方がわかりやすいかもしれません。

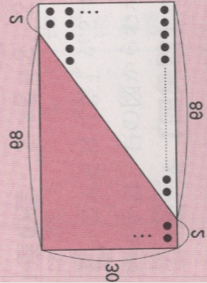
簡潔に説明するなら、こんな感じです（図を自作してみました）。

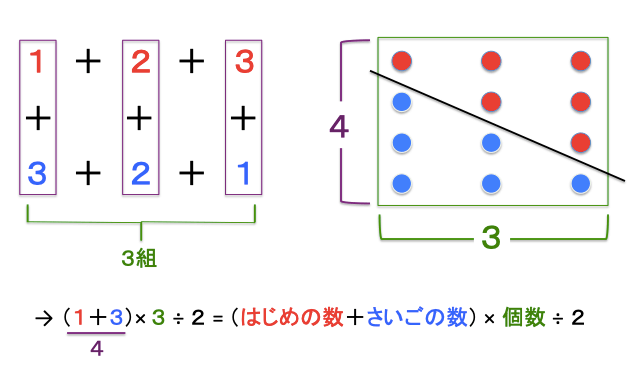
話は飛躍しますが、足し算、掛け算を上記のように、面積で捉えることができるお子様なら、積分の理解も全然大したことはありません。さらに、多重積分（大学の分野？）も同じことだと思います。私は素人ですが、複素数よりも遥かに理解しやすいと、経験的にそのように思います。

積分を学習するのに高校3年生まで待つ必要はないですよね。

時間は有限です。

どんどん進めましょう。

【追記】さらに加筆いただきました。

ガクさん　「受験パズルの攻略法」の続きです。

思うことがあり、三角形の面積が「底辺 x 高さ x 1/2」である理由、錐体の体積が「底面積 x 高さ x 1/3 」である理由を説明してみます。ちなみに、「秘伝の算数　応用編　p76」には四角錐を例に説明していますが、円錐の説明はありません。

（１）三角形の面積が「底辺 x 高さ x 1/2」である理由

まずは、三角形の面積が、底辺 x 高さ x 1/2である理由

（図A）底辺１０cm、高さ１０cm  の三角形（10 x 10 x 1/2 = 50㎠）を、

（図B）のように

「底辺１０cm x 高さ１cmの長方形」（一番下のオレンジ色の長方形）
＋「底辺９cm x 高さ１cm」
＋「底辺８cm x 高さ１cm」
＋「底辺７cm x 高さ１cm」
＋「底辺６cm x 高さ１cm」
＋「底辺５cm x 高さ１cm」
＋「底辺４cm x 高さ１cm」
＋「底辺３cm x 高さ１cm」
＋「底辺２cm x 高さ１cm」
＋「底辺１cm x 高さ１cm」
=５５㎠

の形として考えてみます。

→ 正しい解である５０㎠よりも大きい値をとってしまいます。（５５㎠ ＞ ５０㎠）

（図C）を見るとわかると思いますが、緑の三角形からはみ出した部分があるから、正しい解の５０㎠よりも大きい値をとってしまうわけです。

（図D）そこで、一番下ののオレンジ色の長方形を除いてみました。
この場合は、

「底辺９cm x 高さ１cm」
＋「底辺８cm x 高さ１cm」
＋「底辺７cm x 高さ１cm」
＋「底辺６cm x 高さ１cm」
＋「底辺５cm x 高さ１cm」
＋「底辺４cm x 高さ１cm」
＋「底辺３cm x 高さ１cm」
＋「底辺２cm x 高さ１cm形」
＋「底辺１cm x 高さ１cm」
=４５㎠

となります。

→ この場合は、正しい解の５０㎠よりも小さい値をとってしまいます。（５０㎠ ＞ ４５㎠）

（図E）緑の三角形の内側にすっぽり入り込みますが、隙間があるために、小さい値を取ってしまうのです。

同様に、１００個の長方形（および、その一番下の長方形を除いた９９個の長方形）で同じような計算をさせてみると、それぞれ、50.5㎠（49.5㎠）となります。さらに細かくこの作業を限りなく続けると、値は限りなく５０㎠ に近づくことでしょう。つまり、三角形の面積 = 底辺 x 高さ x 1/2 とみなすことができるわけです。（50.5㎠ ＞ ５０㎠ ＞ 49.5㎠）

（２）円錐で考える

次に、円錐について（最初の図を使い回していますが、横から観察した図だと思ってください。）

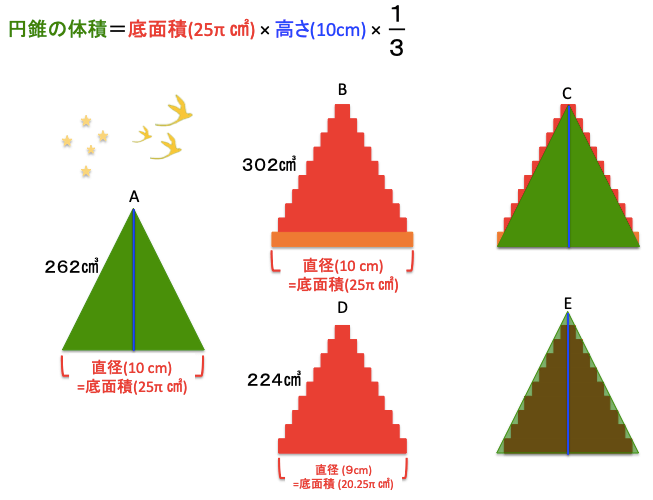
（図A）底面が半径５cmの円 、高さ１０cm  の円錐（５ x ５ x ３.14 x 10 x 1/3 = 262㎤）を、
（図B）のように

「半径５cmの円 x 高さ１cmの円柱」（一番下のオレンジ色の部分）
＋「半径4.5cmの円 x 高さ１cm」
＋「半径4cmの円 x 高さ１cm」
＋「半径3.5cmの円 x 高さ１cm」
＋「半径3cmの円 x 高さ１cm」
＋「半径2.５cmの円 x 高さ１cm」
＋「半径2cmの円 x 高さ１cm」
＋「半径1.5cmの円 x 高さ１cm」
＋「半径1cmの円 x 高さ１cm」
＋「半径0.5 cmの円 x 高さ１cm」
=３０２㎤

の物体として考えてみます。

→ 正しい解の２６２㎤よりも大きい値をとってしまいます。（３０２㎤ ＞ ２６２㎤）

（図C）を見るとわかると思いますが、緑の円錐からはみ出した部分があるのです。
（図D）そこで、一番下ののオレンジ色の円柱を除いてみました。
この場合は、

「半径4.5cmの円 x 高さ１cm」
＋「半径4cmの円 x 高さ１cm」
＋「半径3.5cmの円 x 高さ１cm」
＋「半径3cmの円 x 高さ１cm」
＋「半径2.５cmの円 x 高さ１cm」
＋「半径2cmの円 x 高さ１cm」
＋「半径1.5cmの円 x 高さ１cm」
＋「半径1cmの円 x 高さ１cm」
＋「半径0.5 cmの円 x 高さ１cm」
=２２４㎤　

となります。

→ この場合は、正しい解の２６２㎤よりも小さい値をとってしまいます。（２６２㎤ ＞ ２２４㎤）

（図E）緑の円錐の内側にすっぽり入り込みますが、隙間があるために、小さな値を取ってしまうのです。

同様に、１００個の円柱（および、その一番下の円柱を除いた９９個の円柱）でも同じような計算をさせてみると、それぞれ、２６６㎤（２５８㎤）となります。さらに細かくこの作業を限りなく続けると、値は限りなく２６２㎤に近づくことでしょう。つまり、円錐の体積 = 底面積 x 高さ x 1/3 とみなすことができるわけです。（２６６㎤ ＞ ２６２㎤ ＞ ２５８㎤）

子供の疑問に対してきちんと向き合う

日頃から、子供が疑問に感じるテーマに対して、誤魔化した説明をすることなく、きちんと向き合っていきたいと願い、ガクさんご紹介の「秘伝の算数」を仕事の合間に読んでみたり、中学生、高校生の子供たちに対しても、数学の進捗状況を聞きつつ、大昔に勉強した内容を振り返ったりするわけですが、今回はアウトプットの一貫でコラムを書いてみました。テキストを読み、新しい知見に対しては純粋に受け入れますが、テキストの説明が不足している場合は、私なりの解釈を加え、小学生にでもわかるような図の作成を試み、ここでアウトプットさせていただいているという流れです。もちろん、解説をそのまま載せているわけではありません。表現の間違い等あればご指摘ください。

理屈をよく考えず、ドリルをどんどん進めるモチベーションも大切ですが、時には、先に進みたい気持ちを抑えながら、十分に時間をかけて足元を固めてから進まなくてはならないこともあります。また、高校数学の小難しい暗号のような計算式で躓くことがないように、小学生のうちからさりげなく極限値の考え方について教えておくのもありなのかもしれません。

管理人からのコメント

素晴らしい記事をありがとうございます。

パズルのたとえ話は日常のタスク管理にも通用すると感じました。
私は中学生の頃から、その日にすべき内容を紙に列挙して書いておき、終わった順に取り消し線を引いていました。タスクを消去する瞬間は極めて爽快で、順調に進んだ日は夕食がますます美味しく感じたのを覚えています。

追伸

「ツリーの上に、クリスマス島の旗の南十字星とシラオネッタイチョウという鳥を置いてみました。」といただきました。ご寄稿者様のセンスが感じられます。

ご寄稿者からのご返信

「パズルのたとえ話は日常のタスク管理にも通用すると感じました。私は中学生の頃から、その日にすべき内容を紙に列挙して書いておき、終わった順に取り消し線を引いていました。タスクを消去する瞬間は極めて爽快で、順調に進んだ日は夕食がますます美味しく感じたのを覚えています。」

←小学生低学年用として、塗り絵のごとく、予定表を塗りつぶしていくタイプのタスクシートがあれば良いですね。

関連書籍

本記事で登場した「秘伝の算数」は私も愛用していました。

読み物感覚で楽しめる良書です。

数学好きになること間違いなし。